原标题：有了长度为什么还要定义测度

首先，长度一般是指一维空间，也就是某条线段的长度。

但测度相对应的概念则是n维空间：

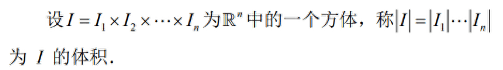
注意上面测度的定义，是相对于n维空间的方体 I 的体积而言的。

然后以积分进行区分。

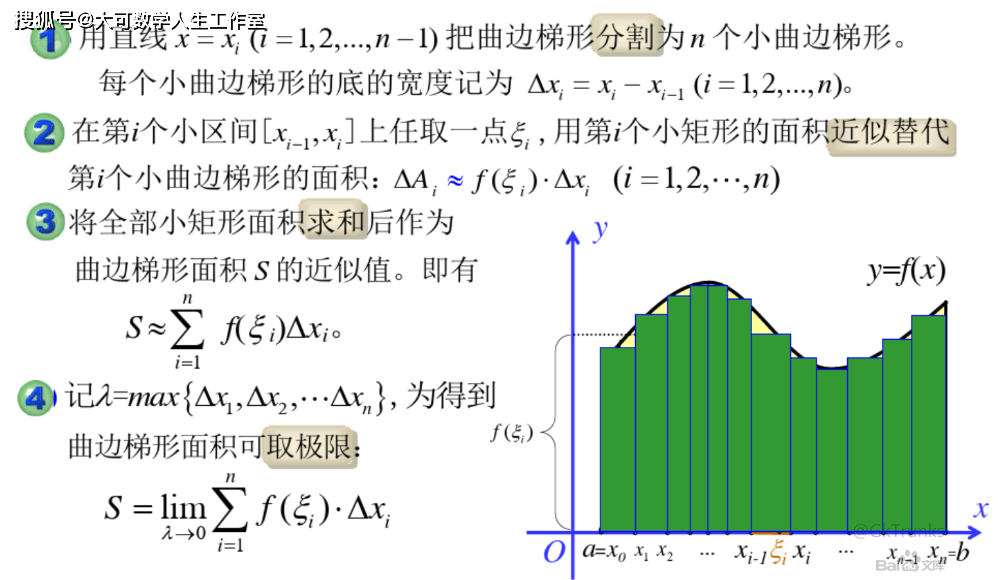
上图中，每一个积分微元里面，f(ξi)的值是固定的。也就是说，在上图定积分的思想里面，是假定每一个区间Δx，不管这个Δxi包括多少个有理数和无理数，都假设它们的函数值是相等的，都是f(ξi)。

测度概念的引入，在于狄里赫雷提出了一个特殊函数。该函数的定义是在实数轴上，当x是有理数时，f(x)等于1，当x是无理数时，f(x)等于0。

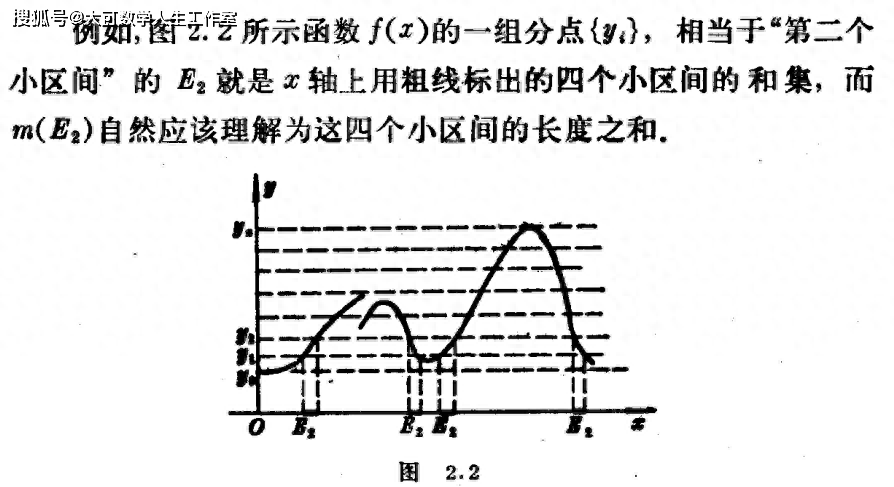
上图曲线假设是狄里赫雷函数曲线，该曲线围成的面积就没有办法按照前面积分的方法进行计算，因为任意一个区间Δx里面既有有理数也有无理数，而有理数对应的高度是1，无理数对应的高度是0（也可以是其它任意数字）。

上图中要求出曲线的面积，就可以假设有理数对应的函数值是yi，然后把x轴上所有有理数的长度相加，这个长度称为测度m(Ei)，然后在两者相乘，即yi(Ei）；对于无理数也一样。最后再把有理数和无理数各自围成的面积相加，就得到曲线围成的面积。

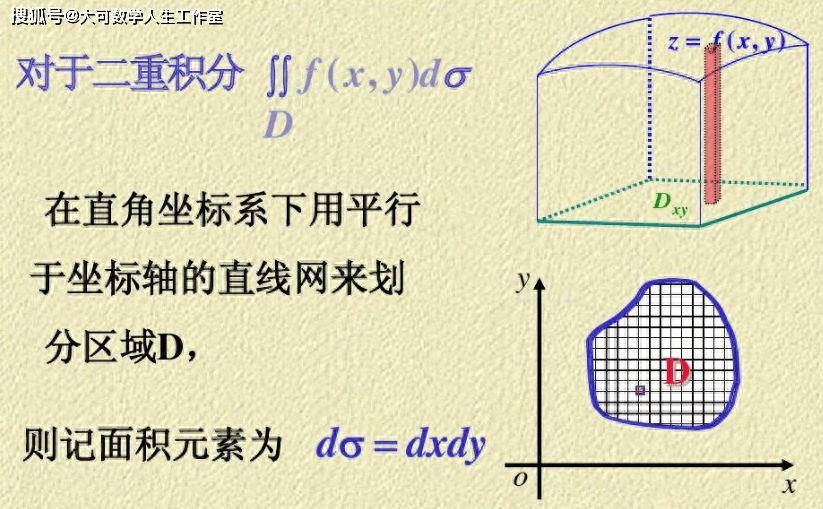
对于上图中三维空间的情形，则意味着XOY平面中，有理数和无理数对应的曲顶柱体的高度不相等，也就是曲顶柱体的高度不连续，这种情况也只能通过测度来计算曲顶柱体的体积。

但我们知道，有理数的测度始终是0，而无理数不是。

由此，测度概念的引入，似乎可以这样理解：

1：为了区分一个函数中有理数和无理数对应的函数值不相等的情形；

2：因为有理数的测度为0，通过测度计算面积或者体积的时候，实际上就是在计算无理数的测度。

来自：万物皆有源