原标题：拉姆齐数与拉姆齐问题新进展

两位数学家表示，他们找到了一个困扰数学界90多年的拉姆齐问题——r(4, t)的近似答案。

撰文 | 佐佑

上世纪20年代，数学家弗兰克·拉姆齐（Frank Ramsey）提出拉姆齐数的概念，这个看似简单的概念，所涉及的却是组合学中异常困难的问题。

拉姆齐数催生了一个被称为拉姆齐理论的领域，这个领域专注于探讨诸如“某个集合需要多大，才能保证出现某个结构”的问题。自20世纪30年代以来，数学家在探索拉姆齐问题方面，几乎没有取得任何可观的进展。

现在，数学家Jacques Verstraete和Sam matthews向预印本网站arXiv上提交了一篇新的论文，表示他们找到了一个困扰数学界90多年的拉姆齐问题——r(4, t)的近似答案。

拉姆齐数与拉姆齐问题

什么是r(4, t)问题？或许我们要先从拉姆齐数说起。

拉姆齐数与单色团概念有关，我们可以通过一个实例来直观地理解拉姆齐数和单色团：将一个有着5个顶点的图的每个点都用线段两两相连，那么我们会发现，用10条线段就可以完成这一步，得到一个5个顶点的完全图（所有顶点都两两相连的图）。接着，将每条边涂成绿色或橙色两种不同的颜色。

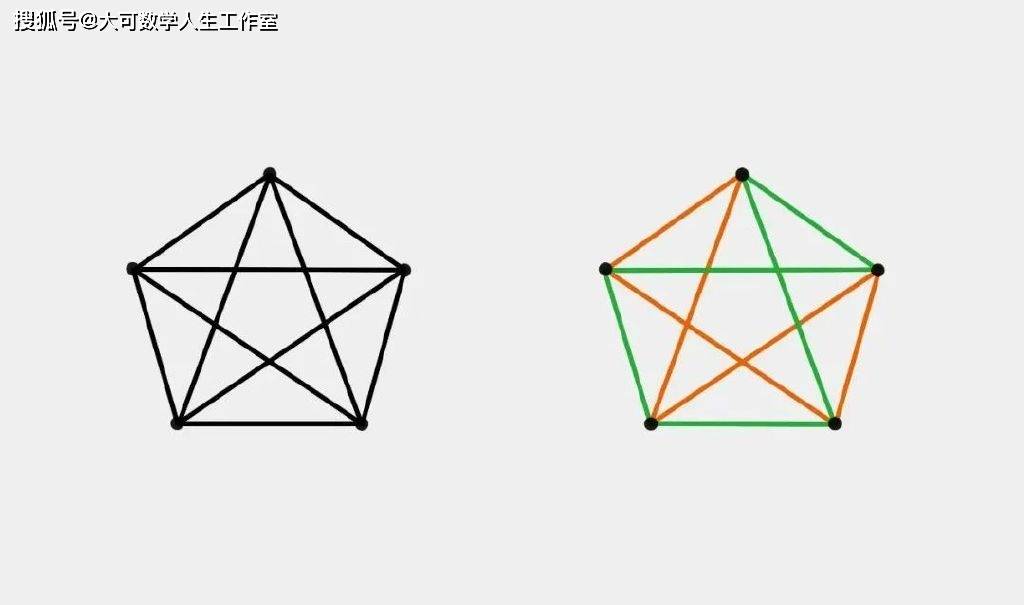
用两种不同颜色为由5个顶点连接而成的完全图的边着色，是有可能避免出现3个顶点由相同颜色的边连接而成的情况的。（图/原理）

现在，问题来了，我们是否可以避免出现3个顶点是用相同颜色的边连接而成的？对于有着5个顶点的完全图来说，问题的答案是肯定的。

接着，让我们将点数从5增加到6。同样，形成一个6个顶点的完全图需要15条边将这些点两两相连，并同样也给这15条边分别涂上绿色或橙色。这时，当我们再去探讨相同的问题时，会发现无论采用什么方法，都不可避免地会得到3个由相同颜色的边相互连接的点。

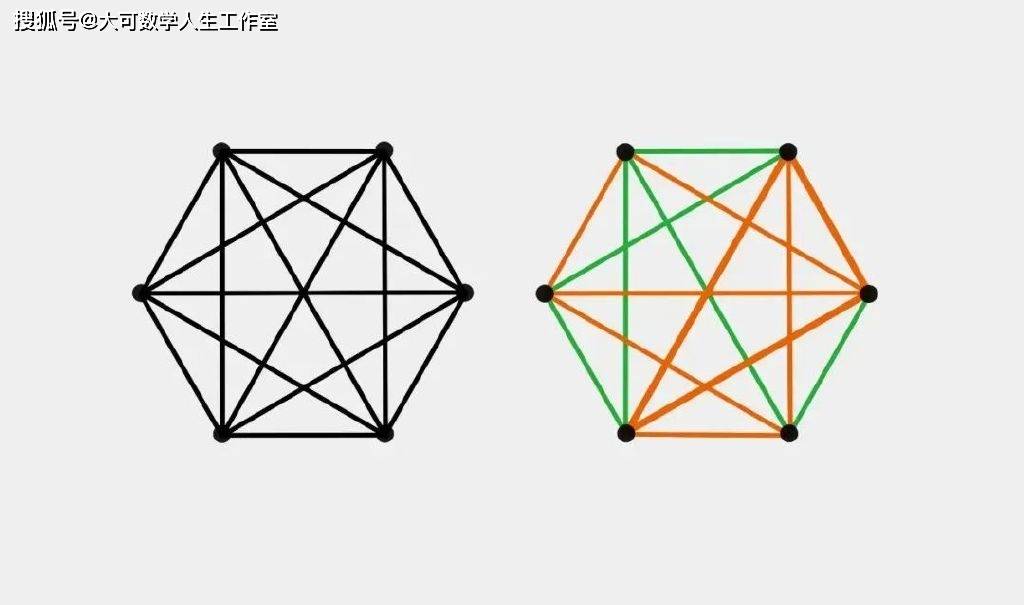
6个顶点的完全图，如果用两种不同颜色为其边着色，必然会出现3个顶点由相同颜色的边连接而成的情况。（图/原理）

这些被相同颜色相连的点，就是单色团。它表示，对于颜色数量为2、大小为3的单色团来说，拉姆齐数为6。它意味着你需要一个至少包含6个顶点的完全图，才能保证这样一个单色团存在。

其实，这个问题还有一个更简单易懂的表达方式，那就是所谓的r(3, 3)派对问题：在一个r人参加的派对中，如果至少要有3个人彼此认识，或者3个人彼此都不认识，那么满足该条件的最小r(3, 3)是多少？从上面的图中，我们知道，r(3, 3)的答案是6。

在数学家知晓了r(3, 3) = 6之后，他们试图求解r(4, 4)、r(5, 5)……等于多少。r(4, 4)的解是18，它是用Paul Erdös和George Szekeres在20世纪30年代创造的一个定理证明的；而r(5, 5)目前仍然未知。事实上，随着单色团的数字增大，拉姆齐数的计算变得越来越复杂。

上界和下界的估计值

为什么看似如此简单的问题这么难以解决？

事实证明，它比看起来要复杂得多。比如，假设数学家知道r(5, 5)的解在40~50之间，如果从45开始，那么需要考虑的图就有超过10234种！这是个令人难以想象的数字，所以数学家很难找到精确的结果，只能进行估计，给出一个可能的取值范围，确保一个任意大小的团的拉姆齐数在某个上界和下界之间。

这也是Verstraete和matthews在新工作中所取得的进展。他们的工作与r(4, t)问题有关，其中t代表不相连的顶点的数量是变量。这个问题已经困扰数学家90多年。

大约四年前，Verstraete与数学家Dhruv Mubayi在研究另一个拉姆齐问题时，发现所谓的伪随机图可以推进对这些问题的现有认知。

1937年，Erdös发现使用随机图可以为拉姆齐问题提供很好的下界。Verstraete和Mubayi发现，频繁地从伪随机图中取样，通常能比随机图给出更好的拉姆齐数边界，可以进一步收紧他们的取值范围。

2019年，Verstraete和Mubayi使用伪随机图求解了r(3, t)。但是，Verstraete难以构建一个有助于求解r(4, t)的伪随机图。于是他开始涉足组合学之外的数学领域，比如有限几何、代数和概率论。最终，他遇到了有限几何领域的专家，Mattheus。

近似值：t的三次函数

他们发现，Verstraete所需要的伪随机图，可以在有限几何中找到。在得到了有助于求解r(4, t)的伪随机图后，仍存在一些其他的数学问题有待解决。最终，他们用了将近一年的时间来处理这些问题，得出了一个近似解：r(4, t)近似于一个t的三次函数。

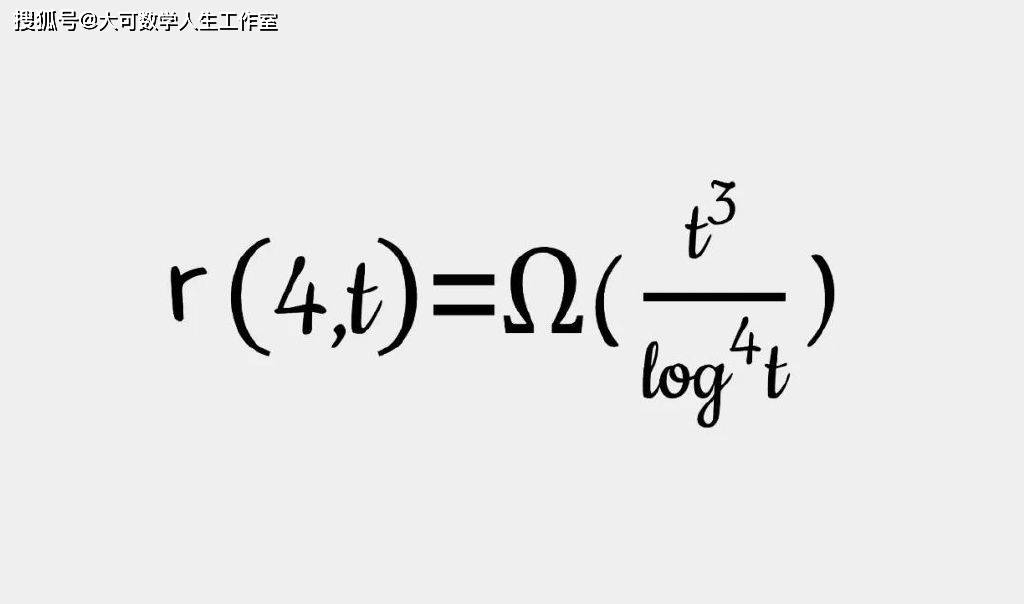
用派对问题的语言可以被表述为，如果想要在一个聚会总是有4个人彼此都认识，或者t个人彼此完全不认识，那么大约需要t^³人在场。需要特别注意的是，是“大约t^³人”，这只是一个非常接近真实情况的估计值，而非一个确切的答案。

参考来源：

[1] https://today.ucsd.edu/story/ramsey-problems

[2] https://arxiv.org/pdf/2306.04007.pdf

[3] https://www.quantamagazine.org/after-nearly-a-century-a-new-limit-for-patterns-in-graphs-20230502/