几何与代数的“数形合一”,源于他的灵光乍现
科学上一道鸿沟的填平,有时需要几个世纪的时间和几代人的努力,有时却在一念之间。
3世纪的古希腊,代数学的成就可以说是相当的辉煌,但生活在那个时代的丢番图,最终也没能彻底跨越具体与抽象之间的鸿沟,建立起一个完整的代数符号系统。那时丢番图所使用的记号是有趣而奇特的。欣赏这种1700年前记号的使用,无疑是一种享受。
大家知道,α,β,γ,δ,ε是希腊文字的前几个字母。那时的希腊在字母顶上加一横,用来代表数,这个数相当于该字母在字母表中的排序。如α可代表1,β代表2,γ代表3,ε代表5,如此等等。
丢番图关于未知数和它们的幂的记号是颇为复杂的: ζ表示未知数,相当于我们今天常用的x,简记为ζ→x,其余记号及现今相应的写法如下所示:
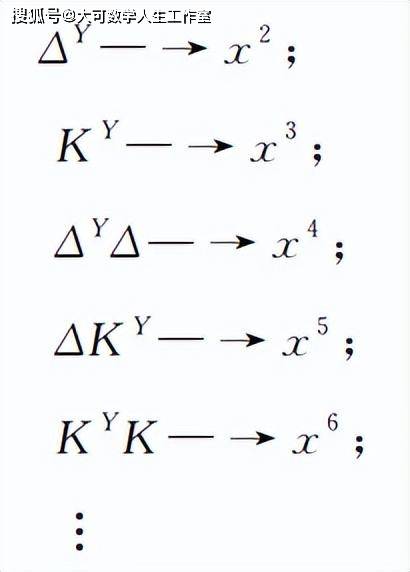
其中Δ和K是“幂”和“立方”相应的希腊文单词的第一个字母。丢番图用“↑”做分隔号,把所有的正项都写在分隔号“↑”的前面,而负项写在分隔号“↑”之后;M表示常数项;一个项的系数一般写于该项之后。
因此丢番图书中的以下一行记号:
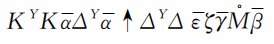
即表示代数式
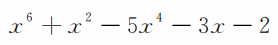
大概由于上面记号的局限性,使得丢番图的成就在中世纪的欧洲,没有能够有效地继承和发展下去。
17世纪以前,几何与代数这两个数学分支采用的是迥然不同的方法。不少人把代数里研究的“数”,与几何里研究的“形”,看成是完全不同的两回事。
1619年,一位才智超群的青年军官,对如何把代数应用到几何上去的问题发生了兴趣。当时部队驻扎在多瑙河旁的小镇,蓝色的天空,绿色的原野,流星在夜空中划过,骏马在大地上奔驰。这一切都引起了这位酷爱数学的青年人的联想: 陨落的流星,驰骋的骏马,它们运动的轨迹应该怎样去描述?
1619年11月10日晚,青年军官躺在床上久久不能入睡。突然,天花板上的一只小虫进入他的视野,小虫缓慢而笨拙地走着它那自以为是的弯弯路。一时间他思绪叠涌: 虫与点,形与数,快与慢,动与静。他似乎感到自己已经悟出了其间的奥秘,但又似乎感到茫然而不可思议!他昏然了,终于深深地进入了梦乡。
俗话说得好: 日有所思,夜有所梦。的确,有时白天百思不解的问题,夜晚的梦却能给人启迪。那天晚上,一个伟大的灵感在睡梦中产生了。
此后几天,这位年轻军官的思绪完全被自己的发现所占据。他找到了一种方法,这种方法可以把几何语言“翻译”成代数语言,从而可以把任何几何问题归结为代数问题加以求解。这就是我们今天常说的解析几何方法,或简称解析法。
创造这一方法的年轻军官,就是后来成名的法国数学家笛卡儿(Descartes,1596—1650)。
笛卡儿

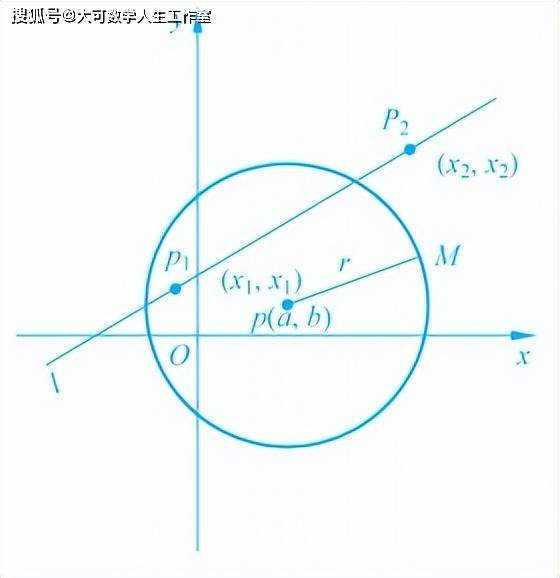
笛卡儿究竟用什么方法把几何语言“翻译”成代数语言呢?现在大家可能已经很熟悉,那就是,在平面上取两条互相垂直的直线为坐标轴,水平的叫横轴,垂直的叫纵轴。它们的交点O叫坐标原点。
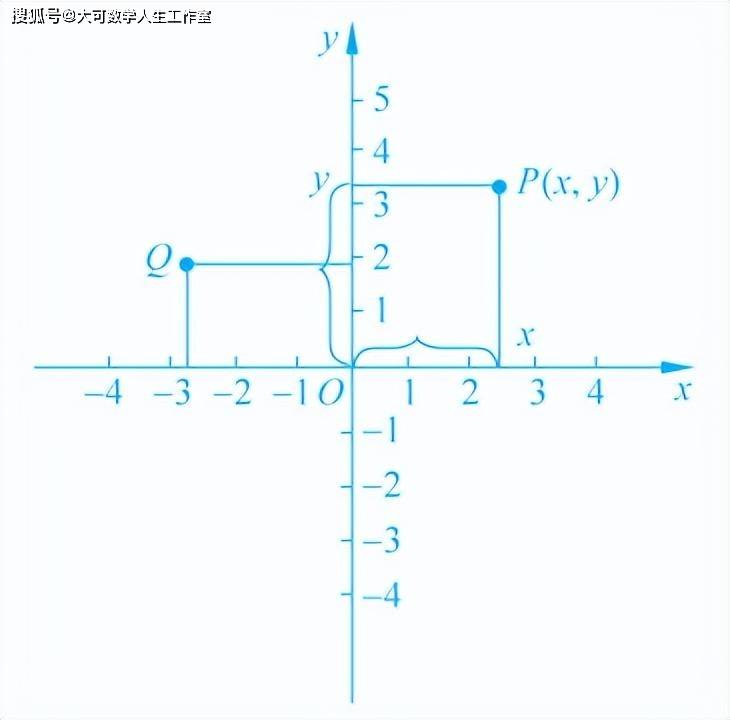
于是,平面上任一点P的位置,都可以用它跟坐标轴的有向距离来决定。P点到纵轴的有向距离称横坐标,常用x来表示; P点到横轴的有向距离叫纵坐标,常用y来表示。此后,便可列出以下几何语言与代数语言的“对译表”。

表中所述的图9.2
这张对译表,无疑可以无限制地编制下去。依靠这样的表,笛卡儿可以把任何几何问题转为代数问题,从而使用代数技巧,化难为易地解决几何问题。
1596年,笛卡儿出生于法国小城拉哈的一个名门望族。他早年受过极好的教育,1616年毕业于普瓦界大学,开始在巴黎当律师,第二年参加了奥伦治公爵的队伍,担任一名文官。
有一次,部队进驻荷兰南部的布勒达城时,一个偶然的机会,笛卡儿成功地解决了一个征答中的数学难题,从此与数学结下了不解之缘。1619年之后,笛卡儿开始致力于解析几何、哲学和物理学的研究声望日高。
1649年10月,笛卡儿接受邀请去为瑞典女王讲授哲学,这位生性怪诞的年轻女王,非要笛卡儿每天清晨5点去为她讲课不可。北欧的隆冬寒风刺骨,酷冷难熬。女王的苛刻要求,超出了这位数学家身体的忍受程度。他不幸染上肺炎,终于一病不起,1650年2月11日,长眠于斯德哥尔摩。
笛卡儿的创造性工作,使整个古典的几何领域,处于代数学的支配之下,从而大大加速了变量数学的成熟。他的主要数学成果,记载于1637年出版的《方法论》一书。
·
来源:《给孩子的数学故事书》
作者:张远南 张昶
