原标题：【物理科普】不用死记硬背就能掌握物理公式，有多爽？！

力和能量是我们看待物理世界的两个不同视角。

面对同一个物理现象，既可以对它进行受力分析，通过牛顿第二定律 F=ma 来求解；也可以找到系统的能量转换关系，利用能量守恒来求解。

那么，力和能量是怎么关联起来的呢？

看一个简单的例子：用一个恒力 F（大小和方向都不变）去推一个质量为 m 的静止物体，然后物体均匀地加速到速度 v。

从力的角度看，物体受到的合外力就是 F，它在这个力的作用下产生了一个加速度 a，然后物体以这个加速度从静止加速到速度 v。不知道大家还记不记得前面关于运动部分的分析。5 个运动相关的物理量 v0、vt、a、t、s，我们只要知道 3 个，就能求出另外 2 个，因为有两个恒等式：

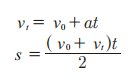
在这个例子里，我们已经知道了 3 个物理量：初速度 v0 为 0，末速度 vt 为 v，加速度为 a。利用上面两个关系式消去时间 t，我们就能得到其他 4 个量的关系：

vt²–v0²=2as。在这个例子里，v0=0，vt=v，代入进去就是 v²=2as，于是距离 s 就可以写成：s=v²/2a。

把距离 s 求出来干什么呢？我们不妨来算一算力 F 和距离 s 的乘积 F·s，也就是算一算力 F 在空间上的累积。

为什么要算这个量呢？待会儿你就知道了。

因为 s=v²/2a，力 F 可以根据牛顿第二定律 F=ma 来算，那么力F 和距离 s 的乘积 F·s 可以表示为：

看到没有，这两个量相乘，刚好把加速度 a 约去了，剩下的结果竟然就是 mv²/2。

是不是很眼熟？这不就是物体的动能吗？也就是说，我们用力 F 乘以这个力作用的距离 s，得到的结果竟然跟物体后来的动能一模一样。

这是一种巧合，还是有什么更深层的含义？

好，上面我们从“力”的角度分析了这个过程，下面再从“能量”角度来看看。

从能量角度来说，物体一开始是静止的，动能为 0，后来具有速度 v，动能为 mv²/2。

也就是说，物体凭空多出了 mv²/2 的动能。那么，这个能量是从哪里来的呢？

从直觉来看，物体会动，是因为有一个力 F 在推它。那么，这个力又是从哪里来的呢？如果是一个人在推物体，那么，为了使出这个力，这个人肯定需要消耗一定的能量。其中一部分能量就给了物体，成了它的动能。

如果是地球在吸引物体，那这个 F 就是重力，结果就成了重力势能转化成了物体的动能。如果是一个电场在推物体，这个力 F 就是电场力，这个过程就是电场能转化成了物体的动能。

当然，题目并没有说这个力 F 是从哪里来的，我们也就无法知道到底是什么能量转化成了物体的动能。

但是没关系，不管这个力是什么力，也不管这个能量到底是从哪里转化来的，我们只要知道用这个力 F 乘以距离 s 就能等效地算出这个动能的大小就可以了。

力作用在一个物体上，并且使物体在力的方向上移动了一段距离，这个过程在物理上叫做功。它是能量从一种形式转化为另一种形式的过程，正如上面提到的人的能量、重力势能、电场能转化成物体动能那样。

虽然这个概念很重要，但是我现在并不想过多地讲这个。你头脑里只要有清晰的能量守恒、能量流动、能量转化的图景就足够了。

有了“力乘以距离就能等效地算出这个动能的大小”的概念后，你会发现很多能量的公式根本不用记，自然而然就能写出来。

不用死记的能量

比如，一个质量为 m 的苹果，在高度为 h 的树上，它具有的重力势能是多少？苹果从树上静止下落，从能量角度来看，就是苹果具有的重力势能转化成了它的动能。而我刚刚说了，力 F 乘以距离s 就能等效地算出这个动能的大小，那自然也就算出了重力势能的大小。在地面附近，苹果的重力为 mg，它从苹果树下落到地面经过的距离为 h。那么，用重力乘以距离得到的 mgh，自然就是苹果具有的重力势能。

同样，在一个匀强电场 E 里，电荷 q 受到的电场力为 qE。那么，在高度为 d 的地方具有的电场能就应该是 qEd。不过，出题人一般会告诉你电势差 U=Ed，这样电场能就可以直接写成 qU。弹性势能稍微麻烦一点，因为弹簧被压缩时，弹力的大小 F 是一直在改变的，F=–kx（k 为弹性系数，x 为压缩距离），并不像重力mg、电场力 qE 那样一直是恒定的。

因此，我们就不能直接用一个固定大小的力乘以距离来表示弹性势能。而应该把弹簧分成很多片，在每一小片里近似认为弹力不变，求出这一小段的弹性势能，再把所有的加起来。这又是微积分的思想，你看看我那篇《你也能懂的微积分》，就知道怎样利用弹力公式 F=–kx 来计算弹性势能的大小了（最终弹性势能的表达式为 kx²/2）。

知道怎么表示重力势能以后，我们再来看看苹果下落这件事。

假设苹果的质量为 m，苹果树的高度为 h。在树上，苹果的动能为 0，重力势能为 mgh ；苹果落地时，重力势能为 0（因为高度h=0)，动能达到最大的 mv²/2。因为能量是守恒的，所以在树上的总能量（0+mgh）就应该等于落地时的总能量（mv²/2+0），即：

把等式两边的质量约掉，g 又是一个常数，这个式子就变成了高度 h 和落地速度 v 的一个关系式。很显然，已知其中一个，立即就能算出另外一个。

当然，如果知道了树的高度 h，就等于知道了运动距离 s，加速度又是已知的 g，初速度等于 0。

所以，我们就已经知道 3 个运动相关的量了，从力学关系出发，一样可以算出下落时间 t 和落地速度 v。这是两种不同的视角，两种方法也都不难。

来源：原点阅读，版权归原作者所有，如有侵权联系删除！

免责声明：自媒体综合提供的内容均源自自媒体，版权归原作者所有，转载请联系原作者并获许可。文章观点仅代表作者本人，不代表环球物理立场。

环球物理

ID：huanqiuwuli

环球物理，以物理学习为主题，以传播物理文化为己任。专业于物理，致力于物理！以激发学习者学习物理的兴趣为目标，分享物理的智慧，学会用物理思维去思考问题，为大家展现一个有趣，丰富多彩的，神奇的物理。

投稿请联系 14511055@qq.com